Tutorial: Avalanche Signature Verification in a dApp
Introduction
This tutorial will show you how to use an Avalanche C-Chain dApp to verify the signature of a message like this that has been signed using the Avalanche Wallet.
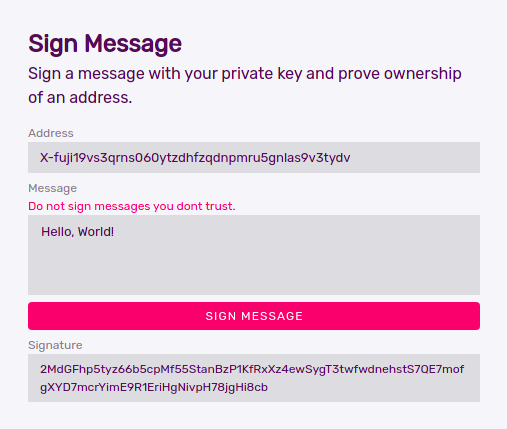
We at red·dev needed to do this for our current software project under development, RediYeti. We have a use-case where we need to verify ownership of an Avalanche X-Chain address before the dApp sends funds related to this address. To prevent fraud, the verification must take place inside of the dApp.
If you need to implement the same kind of signature verification in your dApp, you will find this tutorial useful. You may also find this tutorial useful if you would like to learn how Avalanche signatures work and how cryptography is implemented on the X-Chain and on the C-Chain.
We have included code snippets throughout, and you can find the entire project here. Many steps are involved, but once you understand how they fit together, you will have a deeper understanding of how this aspect of Avalanche—and indeed cryptocurrencies in general—works.
Audience
To get the most out of this tutorial, you will need to have a basic understanding of Javascript, Node, Solidity, and how to develop dApps in Avalanche. You should also know the basics of public key cryptography. Avalanche uses Elliptic Curve Cryptography (ECC) as do Bitcoin, Ethereum, and many others. The ECC algorithm used for digital signatures is called ECDSA (Elliptic Curve Digital Signature Algorithm). If you do not yet know about these topics, see the Resources section at the end for links to learn more.
Why are digital signatures important?
A digital signature system allows you to generate your own private/public key pair. You can then use the private key to generate digital signatures which let you prove that (1) you are the owner of the public key and (2) that the signed message has not been altered—both without having to reveal the private key. With cryptocurrencies, keeping your private key secret is what lets you hold onto your funds, and signing messages is how you transfer funds to others, so digital signatures are indeed foundational to Avalanche.
Overview
At the very highest level, here is an overview of the process we will take you through in this tutorial. First we use a simple webapp to gather the three inputs: signing address, message, and signature. We extract the cryptographic data from them that will be passed into the dApp to verify the signature.
The dApp then verifies in two steps. First, it makes sure that all the values passed to it are provably related to each other. Then, assuming that they are, it uses the elliptic-curve-solidity library, which we have slightly modified to work with Avalanche, to verify the signature.
The dApp returns its result to the webapp which displays it. Of course, in your dApp, you will want to take some more actions in the dApp based on the result, depending on your needs.
(Note: If you're already a Solidity coder, you might think that there is an easier way to do this using the EVM's built-in function ecrecover. However, there is one small hitch that makes using ecrecover impossible: it uses a different hashing method. While Avalanche uses SHA-256 followed by ripemd160, the EVM uses Keccak-256.)
We have set up a demo webpage here.
Requirements
Metamask needs to be installed on your browser, and you need to be connected to the Avalanche Fuji test network (for this tutorial). You can add a few lines of codes to check if your browser has Metamask installed, and if installed, then to which network you are connected. For instance:
function checkMetamaskStatus() {
if((window as any).ethereum) {
if((window as any).ethereum.chainId != '0xa869') {
result = "Failed: Not connected to Avalanche Fuji Testnet via Metamask."
}
else {
//call required function
}
}
else {
result = "Failed: Metamask is not installed."
}
}
Dependencies
- NodeJS v8.9.4 or later.
- AvalancheJS library, which you can install with
npm install avalanche - Elliptic Curve library, which can be installed with
npm install elliptic - Ethers.js library, which can be installed with
npm install ethers
Steps that need to be performed in the webapp
To verify the signature and retrieve the signer X-Chain address, you first need to extract cryptographic data from the message and signature in your webapp, which will then be passed to the dApp. (The example code uses a Vue webapp, but you could use any framework you like or just Vanilla Javascript.) These are:
- The hashed message
- The r, s, and v parameters of the signature
- The x and y coordinates of the public key and the 33-byte compressed public key
We extract them using Javascript instead of in the dApp because the Solidity EC library needs them to be separated, and it is easier to do it in Javascript. There is no security risk in doing it here off-chain as we can verify in the dApp that they are indeed related to each other, returning a signature failure if they are not.
1. Hash the message
First, you will need to hash the original message. Here is the standard way of hashing the message based on the Bitcoin Script format and Ethereum format:
sha256(length(prefix) + prefix + length(message) + message)
The prefix is a so-called "magic prefix" string \x1AAvalanche Signed Message:\n, where 0x1A is the length of the prefix text and length(message) is an integer of the message size. After concatenating these together, hash the result with sha256. For example:
function hashMessage(message: string) {
let mBuf: Buffer = Buffer.from(message, 'utf8')
let msgSize: Buffer = Buffer.alloc(4)
msgSize.writeUInt32BE(mBuf.length, 0)
let msgBuf: Buffer = Buffer.from(`\x1AAvalanche Signed Message:\n${msgSize}${message}`, 'utf8')
let hash: Buffer = createHash('sha256').update(msgBuf).digest()
let hashex: string = hash.toString('hex')
let hashBuff: Buffer = Buffer.from(hashex, 'hex')
let messageHash: string = '0x' + hashex
return {hashBuff, messageHash}
}
2. Split the Signature
Avalanche Wallet displays the signature in CB58 Encoded form, so first you will need to decode the signature from CB58.
Then, with the decoded signature, you can recover the public key by parsing out the r, s, and v parameters from it. The signature is stored as a 65-byte buffer [R || S || V] where V is 0 or 1 to allow public key recoverability.
Note, while decoding the signature, if the signature has been altered, the cb58Decode function may throw an error, so remember to catch the error. Also, don't forget to import bintools from AvalancheJS library first.
function splitSig(signature: string) {
try{
let bintools: Bintools = BinTools.getInstance()
let decodedSig: Buffer = bintools.cb58Decode(signature)
const r: BN = new BN(bintools.copyFrom(decodedSig, 0, 32))
const s: BN = new BN(bintools.copyFrom(decodedSig, 32, 64))
const v: number = bintools.copyFrom(decodedSig, 64, 65).readUIntBE(0, 1)
const sigParam: any = {
r: r,
s: s,
v: v
}
let rhex: string = '0x' + r.toString('hex') //converts r to hex
let shex: string = '0x' + s.toString('hex') //converts s to hex
let sigHex: Array<string> = [rhex, shex]
return {sigParam, sigHex}
}
catch{
result = "Failed: Invalid signature."
}
},
3. Recover the public key
The public key can be recovered from the hashed message, r, s, and v parameters of the signature together with the help of Elliptic Curve JS library. You need to extract x and y coordinates of the public key to verify the signature as well as the 33-byte compressed public key to later recover the signer's X-Chain address.
function recover(msgHash: Buffer, sig: any) {
let ec: EC = new EC('secp256k1')
const pubk: any = ec.recoverPubKey(msgHash, sig, sig.v)
const pubkx: string = '0x' + pubk.x.toString('hex')
const pubky: string = '0x' + pubk.y.toString('hex')
let pubkCord: Array<string> = [pubkx, pubky]
let pubkBuff: Buffer = Buffer.from(pubk.encodeCompressed())
return {pubkCord, pubkBuff}
}
Here is the full code for verification, including the call to the dApp function recoverAddress at the end, which we will cover next:
async function verify() {
//Create the provider and contract object to access the dApp functions
const provider: any = new ethers.providers.Web3Provider((window as any).ethereum)
const elliptic: any = new ethers.Contract(contractAddress.Contract, ECArtifact.abi, provider)
//Extract all the data needed for signature verification
let message: any = hashMessage(msg)
let sign: any = splitSig(sig)
let publicKey: any = recover(message.hashBuff, sign.sigParam)
//prefix and hrp for Bech32 encoding
let prefix: string = "fuji"
let hrp: Array<any> = []
for (var i=0; i<prefix.length; i++) {
hrp[i] = prefix.charCodeAt(i)
}
//Call recoverAddress function from dApp. xchain and msg are user inputs in webapp
const tx: string = await elliptic.recoverAddress(message.messageHash, sign.sigHex, publicKey.pubkCord, publicKey.pubkBuff, msg, xchain, prefix, hrp)
result = tx
}
Recover the signer X-Chain address in dApp
In the dApp, receive as a parameter the 33-byte compressed public key to recover the X-Chain Address.
Addresses on the X-Chain use the Bech32 standard with an Avalanche-specific prefix of X-. Then there are four parts to the Bech32 address scheme that follow.
- A human-readable part (HRP). On Avalanche mainnet this is avax and on Fuji testnet it is fuji.
- The number 1, which separates the HRP from the address and error correction code.
- A base-32 encoded string representing the 20 byte address.
- A 6-character base-32 encoded error correction code.
Like Bitcoin, the addressing scheme of the Avalanche X-Chain relies on the secp256k1 elliptic curve. Avalanche follows a similar approach as Bitcoin and hashes the ECDSA public key, so the 33-byte compressed public key is hashed with sha256 first and then the result is hashed with ripemd160 to produce a 20-byte address.
Next, this 20-byte value is converted to a Bech32 address.
The recoverAddress function is called in the dApp from the webapp.
recoverAddress takes the following parameters:
- messageHash — the hashed message
- rs — r and s value of the signature
- publicKey — x and y coordinates of the public key
- pubk — 33-byte compressed public key
- xchain — X-Chain address
- prefix — Prefix for Bech32 addressing scheme (avax or fuji)
- hrp — Array of each unicode character in the prefix
Then it performs the following steps:
- Gets the 20-byte address by hashing the 33-byte compressed public key with sha256 followed by ripemd160.
- Calls the Bech32 functions to convert the 20-byte address to Bech32 address (which is the unique part of the X-Chain address).
- Verifies that the extracted X-Chain address matches with the X-Chain address from the webapp.
- If X-Chain Address matches then validates the signature.
- Returns the result.
Here is the recoverAddress function that does all this:
function recoverAddress(bytes32 messageHash, uint[2] memory rs, uint[2] memory publicKey, bytes memory pubk, string memory xchain, string memory prefix, uint[] memory hrp) public view returns(string memory){
bool signVerification = false;
string memory result;
bytes32 sha = sha256(abi.encodePacked(pubk));
bytes20 ripesha = ripemd160(abi.encodePacked(sha));
uint[] memory rp = new uint[](20);
for(uint i=0;i<20;i++) {
rp[i] = uint(uint8(ripesha[i]));
}
bytes memory pre = bytes(prefix);
string memory xc = encode(pre, hrp, convert(rp, 8, 5));
if(keccak256(abi.encodePacked(xc)) == keccak256(abi.encodePacked(xchain))) {
signVerification = validateSignature(messageHash, rs, publicKey);
if(signVerification == true) {
result = "Signature verified!";
}
else {
result = "Signature verification failed!";
}
}
else {
result = string(abi.encodePacked("Failed: Addresses do not match. Address for this signature/message combination should be ", xc));
}
return result;
}
Let's take a closer look at its supporting functions and key features.
Bech32 Encoding
We have ported Bech32 to Solidity from the Bech32 Javascript library. There are four functions, polymod, prefixChk, encode and convert, used to convert to Bech32 address.
bytes constant CHARSET = 'qpzry9x8gf2tvdw0s3jn54khce6mua7l';
function polymod(uint256 pre) internal view returns(uint) {
uint256 chk = pre >> 25;
chk = ((pre & 0x1ffffff) << 5)^(-((chk >> 0) & 1) & 0x3b6a57b2) ^
(-((chk >> 1) & 1) & 0x26508e6d) ^
(-((chk >> 2) & 1) & 0x1ea119fa) ^
(-((chk >> 3) & 1) & 0x3d4233dd) ^
(-((chk >> 4) & 1) & 0x2a1462b3);
return chk;
}
function prefixCheck(uint[] memory hrp) public view returns (uint) {
uint chk = 1;
uint c;
uint v;
for (uint pm = 0; pm < hrp.length; ++pm) {
c = hrp[pm];
chk = polymod(chk) ^ (c >> 5);
}
chk = polymod(chk);
for (uint pm = 0; pm < hrp.length; ++pm) {
v = hrp[pm];
chk = polymod(chk) ^ (v & 0x1f);
}
return chk;
}
function encode(bytes memory prefix, uint[] memory hrp, uint[] memory data) public view returns (string memory) {
uint256 chk = prefixCheck(hrp);
bytes memory add = '1';
bytes memory result = abi.encodePacked(prefix, add);
for (uint pm = 0; pm < data.length; ++pm) {
uint256 x = data[pm];
chk = polymod(chk) ^ x;
result = abi.encodePacked(result, CHARSET[x]);
}
for (uint i = 0; i < 6; ++i) {
chk = polymod(chk);
}
chk ^= 1;
for (uint i = 0; i < 6; ++i) {
uint256 v = (chk >> ((5 - i) * 5)) & 0x1f;
result = abi.encodePacked(result, CHARSET[v]);
}
bytes memory chainid = 'X-';
string memory s = string(abi.encodePacked(chainid, result));
return s;
}
function convert(uint[] memory data, uint inBits, uint outBits) public view returns (uint[] memory) {
uint value = 0;
uint bits = 0;
uint maxV = (1 << outBits) - 1;
uint[] memory ret = new uint[](32);
uint j = 0;
for (uint i = 0; i < data.length; ++i) {
value = (value << inBits) | data[i];
bits += inBits;
while (bits >= outBits) {
bits -= outBits;
ret[j] = (value >> bits) & maxV;
j += 1;
}
}
return ret;
}
Verify X-Chain address
It is a simple step, but it is very important to check to see if the extracted X-Chain address from the public key matches with the X-Chain address that was passed from the webapp. Otherwise, you may have a perfectly valid message signature but for a different X-Chain address than the webapp requested. Only if they match can you proceed to verify the signature. Otherwise, return an error message.
Validate signature
For verifying the signature, we start with this Solidity project on Elliptic Curve.
However, this project uses the secp256r1 curve. As Avalanche uses secp256k1 curve, we need to modify the constant values based on this curve. (Note: Since modifying cryptographic functions is risky, these are the only modifications we have made.) The constants now look like this:
uint constant a = 0;
uint constant b = 7;
uint constant gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798;
uint constant gy = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8;
uint constant p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F;
uint constant n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141;
The key function we need is validateSignature.
function validateSignature(bytes32 messageHash, uint[2] memory rs, uint[2] memory publicKey) public view returns (bool)
validateSignature takes the same first three parameters as recoverAddress:
- messageHash — the hashed message
- rs — r and s value of the signature
- publicKey — x and y coordinates of the public key
Finishing up
After performing these tests, the dApp returns its decision whether the signature is valid or not to the webapp, and the webapp is then responsible for showing the final output to the user. As we mentioned above, in your dApp, you will probably want to take further actions accordingly.
Resources
Here are some resources that can use to teach yourself the subjects you need in order to understand this tutorial.
- This is a useful documentation from Ava Labs on cryptographic primitives: https://docs.avax.network/build/references/cryptographic-primitives
- Here is a great YouTube video by Connor Daly of Ava Labs on how to use Hardhat to deploy and run your smart contract on Avalanche network: https://www.youtube.com/watch?v=UdzHxdfMKkE&t=1812s
- If you want to learn more on how the private/public keys and the wallets work, you may enjoy going through this awesome tutorial by Greg Walker: https://learnmeabitcoin.com/technical/
- Andrea Corbellini has done great work explaining Elliptic Curve Cryptography in detail in her blog post: https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/